Pitch/Partial Tracking的新方向 - 胤霖

-----------2010.12.30-------------------

簡單測試使用已知和未知的initial templates，單獨分析一個time frame。(frame size = 8192, initial number of templates = 4)

W未知(random)：

W已知(由上而下分別設templates初始音高為 - G2, D3, B3, A3)：

如果W沒有給適當的資訊，training的結果就整個都很亂；反之，結果好很多。

-----------2010.12.28-------------------

論文報告：
Non-negative Matrix Factor Deconvolution; Extraction of Multiple Sound Sources from Monophonic Inputs
ppt

-----------2010.12.23-------------------

接續上次的結果，加上限制條件的同時再多加一個random不受限的template：
(藍色-result of standard NMF；紅色-再加harmonicity & random tamplate)

-----------2010.12.10-------------------

"但是基本partial energy分配沒多大變化，可以解釋一下嗎?"
老師提到的這個問題，是不是指被抑制的partial們沒有影響到其他template?
我的想法是這樣：
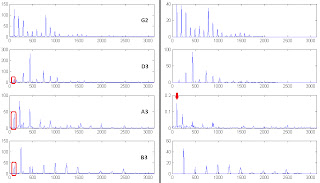
在這次的例子中，每個templates裡都有一根很明顯的G2基頻(下圖紅色圈圈示)，但是加上限制後，這個能量被抑制了，結果全部集中到A3裡，所以最後A3中G2基頻的能量反而特別高(此外，也許連其他雜訊也都跑到這裡了)。

我用cooledit將原本的音檔分成兩半(剩下前八個音，前八個音和後八個音是重複的)，再把A3這個音直接刪掉，如下圖(譜)。

以這一段音檔測試有加和沒加限制的結果。lamda設為1。initial template = 3。

上圖左是沒加上限制，右邊有。
結果和上次相似，圖右的B3也是雜訊能量增加。

-----------2010.12.7--------------------

簡單的測試一下harmonicity的必要性:
測試的曲目為巴哈無伴奏前16個音，使用4個templates，在第一次run完NMF演算法後，分別以這4個templates中的4組partial groups來作harmonicity的限制。
限制的方法(很久以前報的)，在原本的cost function中加上一個計算雜訊能量的項，如下式:

S用來取出W中，不為harmonics的能量。

其中的lamda我還沒有去計算出正確的值，以下的結果以1/8和2代入。
lamda = 1/8

上圖左沒有限制，右邊有加上harmonic限制。
加上限制後，不在各個template的harmonics上的能量變小，但都還在。

lamda = 2

上圖左沒有限制，右邊有加上harmonic限制。
lamda值增加後，除了A3這個template雜訊的能量反而增加，其他的不在harmonics上的能量都被消掉了。
不過以上的結果，可能因為我使用的update rules而有錯誤，之後會確定一下公式的正確性並找出適當的lamda值。

-----------2010.11.30-------------------

論文報告：
Nonnegative Matrix Factorization with Markov-chained Bases for Modeling Time-varying patterns in Music Spectrograms
ppt

-----------2010.11.2--------------------

論文報告：
TIME-DEPENDENT PARAMETRIC AND HARMONIC TEMPLATES IN NON-NEGATIVE MATRIX
ppt

-----------2010.4.27--------------------

繼續上次的實驗，把相同的compoment加再一起。
加完後W變成:

以此W去測試，結果如下:


左邊為X矩陣，右邊為W矩陣。
因為第4個W較雜亂，所以把她刪除看看結果(第7個取代第4個):


結果和上一張圖的幾乎相同。
分開過後的W很多值都變成0，在train後也不會再有值，也因為這樣partial的形狀都不太改變了。

-----------2010.4.14--------------------

針對巴哈的小步舞曲第三節，原本會有在同一template觀察到兩個partial group的問題，測試結果如下。
第三小節的譜:

原本作出來混合的W和其對應的X :


如圖所示，第2、5、6個template都有混合的音。
新的W長這樣:

再次train的結果(W和其對應的X):


除了第4個還是很雜亂，其他的templates都保持很好的partial的形狀。

-----------2010.3.19--------------------

上次的實驗結果不盡理想，所以做了以下的修改：
1.Input較小的錄音片段，每次大約1到2小節。
2.檢查用來做template的西班牙錄音，看看他的諧波結構是否影像NMF結果
3.要保留較好的W時，一次保留較少的template。

一開始我先試了一下上次的小步舞曲那個片段的第四小節(共4個音)：
先檢查西班牙的錄音，我選了C4、D4、E4、F4這四個notes來看，下面是他的頻譜的放大圖：


用這四個音當作templates去算第四小節的結果：


因為部分在基頻前會有小小的peak(能量滿小的)，將其變小如下：


再用這四個修改過的音去算第四小節：


從圖上看來差不多，也許因為那些多出來的peak能量很小，影響不大；所以template算出來不好看應該不是這個原因導致。


接著對於第一次train出來的W，我保留了第一個較好的，再丟回去train一次：



看剛剛的圖有些許不同，第二的template變得比較明顯，不知道算不算是有變好？

然後我算了一下問題最多的第三小節(共6個音)，這個小節一直都有兩個音在同一個template或是miss音的問題：
以下是第一次train：



然後再分別測試只保留1st和同時保留1st和3rd的template。
以下是保留了第一個template後再丟回去的結果：


以下是保留第一個和第三個template後再丟回去的結果：



兩個結果看起來都差不多。音都還是混在一起。

最後，老師問過說如果Ｗ丟random的會怎樣，我分別對這兩小節丟random的W算：
第三小節：


第四小節：


得到丟random也是可以算出結果，而且算出來X的位置還滿準的，不過W沒那麼明顯，第四小節比較好一點，第三小節就看不太出頻率了。

-----------2010.3.10--------------------

為了要改善NMF這個演算法，使它在pitch detection上有更好的辨識度，試著找出、修改他的cost function，主要是希望可以從train的過程中找到好的templates(W矩陣)。現在定義一個有明顯諧波形狀的template是好的，所以在修正時也是讓W可以update成這個樣子最好。然後決定train出來的W哪些是要的哪些是不要的。
要保證選擇好的templates是有用，所以我在之前作過的曲子中把好的W取出來再丟回去作一次，看看結果如何。

以下是我以之前作過的Bach - Minuet01的錄音片段作的測試：
(共13個pitch)


上面是第一次跑NMF後的結果(圖都有經過放大)。
初始的templates：C4、D4、…A5、B5 (14個)
按照定義選擇諧波形狀較明顯的templates出來，這邊我是選取第1、2、4、5、6、7、9、10、11、12個template當作好的(從W的圖上可以看到這些都是諧波較明顯的)，再回去測試一次。



上面是第二次測試的結果。
templates：剛剛取的10個再加上E4、C5、A5、B5。



上面是第三次測試的結果。
templates：第一次取的10個再加上E4、C5、A3、B4。

有打X記號的templates是看起來不好(我認為)的W，從第二和第三次的結果中看到train完結果沒有變不好，但似乎也沒有變更好，miss的pitch還是沒有被找到，而兩次後來加的templates經過training後幾乎一樣。

-----------2010.1.29--------------------

因為之前拼湊出來的巴哈小步舞曲，在以同一種音色的template情況下，仍然無法每個音都正確找出，推測是出錯的note音量太小導致，所以現在嘗試找強弱變化較大的歌曲來作看看。

測試曲目：Debussy／clair de lune → 音檔
選取其中彈奏有漸強的一個片段：

共51個音符，19個不同的notes。 (修正標錯的音高, 2010/3/10)

測試結果：
Template：C4、C4#、D4……B5，共24個。
上圖是X的結果。紅色圈圈指的是多出的peak。 (修正上圖第2個X的錯誤, 2010/3/10) 我把有找對的音符標記起來，橘色圈起的是對照有符合的音符。
圈圈是對的，三角形是有少peak的。雖然有的template有update出某個頻率，但是對照其對應的X和譜上的位置都對不太起來，就當成是沒找到。
在update完的template中，miss了C3#、B3、C4、F4、E5、B5。

從上面的結果來看，前半部音量較小的部分，滿多都有被找出來的，可能是這段的音量前半部都是比較小聲而後半部都是比較大聲的關係。而在後半部像是C5#、E5、G5#、B5這幾個相對比較小聲的音(我自己聽起來)，有些是被miss掉有些是位置對不太起來。
所以針對後半部，再把曲子分成兩半，對後半部這段旋律作測試。(後半有12個不同的音)

測試結果：
Template：C4、C4#、D4……B4、C5，共13個。
上圖為X的結果，紅色圈圈是缺少一個peak的地方。 橘色圈起處是對照後符合的音符。

本來以為音樂片段短一點效果會比較好，但跟上一個比起來結果更奇怪了…，miss的音更多。也許是初始的W設得不好？

上面的實驗我都是用Kawai RX2_k5的鋼琴錄音作為templates，應該要試試看用其他的鋼琴錄音。
-----------2009.12.31-------------------

論文報告
paper
ppt

-----------2009.12.21-------------------

上次使用同一個樂器，卻還是出現錯誤的問題，DNA學長說可以多增加一個無關的template，看是否讓錯誤的資訊都收集到此template中。
以下是測試的結果:



第11和13個template是原本出錯的template，第14個是新增的。
增加以後出錯的兩個在時間上的peak就變明顯，也可以從W矩陣中看出頻率大小。
但是第13個template(E5)還是會有另外一個聲音的頻率出現(C4)。
而C4和E5在演奏時是同時出現的。


不過除了出現C4這個問題，其他的音都有被正確的找出。

-----------2009.12.16-------------------

這次我用了兩種方法來測試template:
1.使用已有的鋼琴錄音拼成曲子來當作測試的音檔。
2.用相同的template測不同的音樂。

以下是結果:
1.使用已有的鋼琴錄音拼成曲子來當作測試的音檔。曲子選自Bach Minuet NO.1的片段；鋼琴錄音為Kawai RX2 k5。
左邊是x矩陣，右邊是W矩陣，後面標示的數字是他的頻率和對應的note，"問號"是不能明顯看出其頻率是多少。
感覺做完的結果並沒有比較好，反而有更多component放了兩個音的情形，觀察了拼湊的片段的頻譜，在音跟音之間的能量很大，可能是因為我在連接時沒有接好。


所以我把能量大的部份去掉再試一次，得到的結果:


只顯示x矩陣的圖和頻率。
除了miss掉C5和E5以外，其他都是正確的。而miss的C5和E5應該就是打問號的那兩個component。

2.用同一份template去測Bach Minuet NO.1的另外一個片段。



圈起來的部分是不該出現peak卻出現peak的位置。


打三角形的component是這兩個音在不該有peak的時候出現peak，打X的是看不出頻率的，塗紫色的兩個component是這兩個音被update成相同的音，他們在頻率上有一點點偏差，但是時間上出現的peak位置差不多。

另外，針對上次的實驗，有兩個音放在同一component的問題，我提高他update的次數看有沒有改善，結果是沒有，還是一樣有這個情形。改將原本的音檔切成兩半，分別來測。


前半是到第二小節的第2個音，後半是第二小節第2個音到最後。



左半邊是前半部的X矩陣的圖，右半邊是後半部的X矩陣的圖。


上圖是前半部，下圖是後半部。
可以看到沒有兩個音放到同一component的情況了。
而塗紫色和藍色的區塊，是指這兩個component被分成相同的note，他們頻率有點不同，但是在時間上的位置差不多。除了這個問題和有些音看不出頻率以外(後半部miss掉D5)，其他都分得很正確。

問題:
上次報的paper提到，如果template的個數比受測試音檔的音多的話，多出來的template和其對應的x矩陣的值都會很小，稱為non-note component，但是我測試出來的結果沒有這個現象，如上面的測試，template是13個，受測試的音為8和11個，多出來的component雖看不出頻率是多少，但是和x矩陣的數值都還是很大。

-----------2009.12.4--------------------

之前老師提到說，template可以有兩種做法，一種是直接將一首曲子的音切下來當template，也就是鋼琴的音色會相同(如果曲子鋼琴演奏的話)；另一種就是使用不同音色的錄音當作template，看看是不是會影響結果。
目前我做的實驗，曲子和template都是先以鋼琴音樂來測試，template是從西班牙的鋼琴錄音拿來放的，一次放一個八度或是放曲子彈奏音的範圍，可以有很多種放的方法，實驗的目的是希望定義出最好的template，找出哪些音可以由哪些template train出來，對各種曲子的pitch detection有好的幫助。

以下是目前簡單的測試結果
曲子的片段來自: Bach Minuet No.1 on Victor piano by Sony PCM-D1


1. template: 未知的piano (C1, F#1, C2, F#2, …, F#6)



錯誤: 第7,10,11個column將兩個音放在同一個component，第3個column在未彈奏此音的位置出現peak。

2. Kawai RX2_k5 (from G3~E5)



錯誤: 第1個column將兩個音放在同一個component，第6個column在未彈奏此音的位置出現peak。

3. Kawai RX2_k5 (from C4~B4)

錯誤: miss G3 and A3
另外，因為template的個數小於歌曲出現的音的個數，所以update完後，多個音會被分配到相同的component中。

接下來就是把已經有的錄音拼出歌曲，再拿來用NMF測試看同音色的結果如何，也可以用不同音色的template測試看看。另外我想可以拿同一個template對不同的曲子測，也許比較可以看出各個template update的效果。

-----------2009.11.28-------------------

討論過後，現在W放的內容很重要。
矩陣再update時，我們無法控制他會update出怎樣的結果，若note在一開始就被計算錯了，後面再出現這個note時很可能繼續錯下去，就會找不到。還有八度音甚至不是八度音也可能會被分到同一個component的問題。所以先要分析出來哪些template是好的要用，哪些是不好的就不要用。

接下來工作就是用曲子下去測試看看，找出合適的template出來。

-----------2009.11.25-------------------

NMD 的 implement：
　　再簡單說明一下NMD的algorithm，給一個聲音的訊號存進矩陣Y，NMD的目的就是尋找出兩個矩陣W和X，使得Y≈W∙X。其中，W∙X重建的Y’與Y越相近越好。W放的是basis function(harmonic templates)，X放可最佳重建Y的係數。此三矩陣都必須是非負矩陣。
　　在這次的實作，使用的樂器是鋼琴，W放12個不同的鋼琴音符作為templates，Input data Y也是由這12個音檔作組合，X則是先放一些正整數做測試。

實驗：
1. 輸入為單音
上圖和下圖分別為原始的y和reconstruct的y，重建的y與原本的y每一個bin的頻率位置相當接近。


下圖的每一條線表示x矩陣中的每一列。圖中，較大的row的值(黑色的data)，正好是輸入的音對應的row的值。


下圖為與上述較大的row在w矩陣中相對應的column值，得到f0與輸入之音檔相同。


2. 混合兩個不同的聲音輸入(相當於同時彈奏)
reconstruct y與y的頻率位置大致上是接近的。


但是從x矩陣(下)看，擁有較大值的row對應的音並不是輸入的兩個音。應該是因為兩個音同時發生，不夠明顯，NMD無法辨識出來。


3. 將兩個不同音高的音相間排列當作輸入
原始的y與 reconstruct y的 頻率位置幾乎相同。


在x矩陣中，與混合的兩個音相對應的row值大小(淡藍色和綠色的data)，也較其他的大一些。此外可以看到，上方的圖為混合音檔的spectrum，x矩陣的row可以表現原始音檔時間軸上的頻率變化。


w矩陣計算出來的f0，也與輸入音檔相同。


以上呈現的結果都是讓x矩陣的每一個row放相同值，結果還是可以找到正確的f0。另外測試x矩陣在錯誤的音對應的row上放較大的數，結果也是可以找到正確的f0。

遇到的問題：
1. 照理說隨著update的次數越多次，y和reconstruct y之間的差距應該越來越小，但是目前cost function算出來的值卻不會慢慢收歛，而是有時變大有時變小。
2. x矩陣中，正確的音對應的row應有較大值，但隨著update的次數增加，錯誤的音對應的row也會慢慢變大。
跟DNA學長討論了一下，以上兩個問題應該都是跟cost function有關，接下來會修正cost function看看是否會改善。

-----------2009.10.15-------------------

論文報告
Real-Time Pitch Determination of One or More Voices by NonnegativeMatrix Factorization
ppt
-----------2009.10.9--------------------

我根據ICA作了一個例子，這個例子我是先將兩個wav檔mix在一起後，再利用ICA找出他原本的音源。我用的是鋼琴音樂，mix成三筆資料input，output出兩個independent component。
toolbox：FastICA ( http://www.cis.hut.fi/projects/ica/fastica/ )。

做出來的結果：

原本的音檔1
music_Input1

output的IC1
music_Output1


原本的音檔2
music_Input2


output的IC2
music_Output2



學長說因為MATLAB會把聲音變大，所以一開始IC輸出成wav檔的時候，有些部分就被切掉，導致聽起來音樂像有雜音一樣很吵，因此把輸出的值全部除以一個整數讓他的能量變小來改善，最後得到的結果，除了比較大聲以外，聽起來幾乎是和原本的音檔一樣。

-----------2009.9.23--------------------

關於ICA(Independent Component Analysis)：

　　ICA起源於”cocktail-party problem”。在宴會中有各種發出聲音的來源，藉由在不同位置收集到的聲音混合訊號，來統計分析出不同的音源，即是ICA的目的。ICA是解決blind source separation(BSS)的一種方法，因為聲音的來源以及其混合的方式都是未知的所以叫做blind，BSS可以復原這些音源訊號。
　　舉例來說，假設一個房間裡有三個人同時說話(聲音的來源)，記為S1(t)、S2(t)、S3(t)，另外也有三個麥克風收集三個不同的混合訊號，記為X1(t)、X2(t)、X3(t)，因為每個麥克風收集到的混合訊號是音源的線性組合，便可列出以下的式子：

X1(t) = a11 S1(t) +a12 S2(t) + a13 S3(t)
X2(t) = a21 S1(t) +a22 S2(t) + a23 S3(t)
X3(t) = a31 S1(t) +a32 S2(t) + a33 S3(t)

其中a11、a12、a13、a21、a22、a23、a31、a32、a33 均為常數。
也就是說，ICA的模型可以寫作：

X = A S

其中X = [ X1, X2, … , Xn ]T；S = [ S1, S2, … , Sm ]T；A為一個未知的n*m的矩陣。
S即為independent components。

ICA的假設和限制條件：
1. 假設independent components為獨立的。
　　這是ICA的原則，而隨機變數是否獨立，可由其機率密度(probability density)來定義，令P(y1, y2, … ,yn)為yi的joint probability density function(pdf)。

yi are independent <=> P(y1, y2, … ,yn) = P(y1) P(y1) …P(yn)

2. Independent components 必須是nongaussian分配。
3. 為了簡化運算，假設未知的混合矩陣為方陣。
　　即矩陣A為n*n矩陣。

計算ICA的方法：
1. Maximization of Nongaussianity
2. Maximum Likelihood Estimation
3. Minimization Mutual Information

References：
1. Aapo Hyvarinen, Independent Component Analysis, John Wiley & Sons.

-----------2009.9.15--------------------

about PCA : ppt


-----------2009.8.18--------------------

論文報告
Adaptive oscillator networks for partial trackingand piano music transcription
ppt

-----------2009.8.16---------------------

我把我看的一些東西先放上來。
先簡單的說明一下PCA(Principal component analysis)的架構。

PCA主要的功能有：
1. 能將資料簡化，將多個有相關的變數簡化成少數幾個互不相關的component。
2. 找出的這些principal component為多個變數的線性組合，可以保有原來這些變數大部分的特性
3. 就是對於較重要的變數給予較大個權重，較不重要的的變數給予較小的權重的一種方法。

　　而PCA的分析方法，是利用資料變數Ｘ的covariance matrix，找出其eigenvalues λ1. λ2…λn和對應的eigenvectors w1. w2 …wn。最大的eigenvalue λ1對應的eigenvector w1乘上變數Ｘ即稱為first principal component；第二大的eigenvalue λ2 對應的eigenvector w2乘上隨機變數Ｘ稱為second principal component…以此類推。

Principal component 解釋資料的能力：
第i個principal component對原來的變數的解釋比例為

　　　　　　　　　　λi / (λ1 +λ2 + …+λq +…+ λp )

若取出q個principal component 來解釋原有的p個變數，其解釋比例為

　　　　　　　　　　(λ1 ＋λ2 + …+λq ) / (λ1 +λ2 + …+λq +…+ λp )

λ為eigenvalue。
　　這樣一來，選取principal component的數目就很重要了。為了簡化資料量，而選取較少的principal component，原來變數的特性較無法保持，反之，選取較多的principal component雖可以保有較完整的變數特性，但即失去簡化的目的。
選取的方法：

　　　　　　　　　　λ1 >λ2 > …>λq >λq+1 =λq+2 = … =λp

　　將eigenvalues由大到小排列，檢查若最後(p-q)個eigenvalues相等，表示最多可以取前q個principal components即可。

PCA的幾何意義：
一筆資料x的散佈圖如下：


　　而first principal component 的權重就是要找出一個方向，使得這些資料點在此方向的投影變異數最大。如下圖中的U、V方向，所有的點在U方向的投影較在V方向的投影分散，可以較明顯看出各點的差異，也就是說U方向比V方向更可以解釋原來的資料變異。


References：
1. Aapo Hyvarinen, Independent Component Analysis, John Wiley & Sons.
2. 陳順宇(2005)，多變量分析(四版)，華泰書局。

-----------2009.8.16---------------------

我把原來的串複製過來，之後的進度會更新在這裡。

雖然文森學長的work做得很好, 但是我們的心中有一點點缺憾, 那就是學長的方法, 除了WGCDV是以前AL學長做的之外, 多半還是來自其他世界上其他的研究者的想法, 縱使為bff學長所開發的High Order HMM. 而過去我也曾經講過, 利用HMM來做tracking似乎不做第二人想, 但是我們除了HMM之外, 能有其他的創見嗎?

文森的Pitch/Partial Tracking

這一點, 我跟DNA學長聊過, 在過去, 我們利用Partial Group似乎得到一些效果, 不過一切的方法似乎比較像是在做影像處理或圖形識別的研究, 也就是試著找所謂的Feature(特徵), 然後用HMM的方式把他們在時間軸上連起來. 但是老實說, 我對影像類的特徵找法不是太有好感, Heuristic或Empirical是我一直用來形容這類方法的名詞, 我對Neural Network的感覺也是如此.

這讓我希望回到用Data Decomposition的比較正統的數學方法來定義Features, 可是怎麼做呢? 我沒十足把握, 所以這一篇不好寫.

一般的數學做法是找eigenvectors, 利用eigenvectors來當tracking(可以是HMM也可以不是)用的Features似乎可行, 不過在我們要對付的問題上, 一般的decomposition的方法卻可能會有問題, 要是可以, 那麼PCA(Principle Component Analysis)或ICA(Independent Component Analysis)的方法就可能派得上用場. 不過, 因為八度音, 甚至五度關係都會讓這類方法破功, 其原因我就不在這裡細講. 因此在這裡我們要定義的Feature Vectors一定有別於一般Linear Algebra中的eigenvectors, 而如何找到演算法來算這Feature Vectors以及如何避開八度與五度的問題是關鍵所在.

所以胤要對付的問題的真正解法在哪裡需要我們一起努力尋找, 而這一類問題要做得好, 數學要有一點底子, 別忘了, Higher Order HMM Tracking是數學系出身的bff學長想出來的. 這讓IRCAM與SCREAM首次在MIREX裡勝出.

MIREX2008 Multiple F0s estimation

我想, DNA與我會多花一點心思在這個問題上面, 請胤想法子趕快學好Matlab, 因為我不希望花太多時間自己寫matlab裡已經有的東西.