HHT – Hilbert Huang Transform

Key words : Hilbert-Huang transform, Hilbert spectrum, Hilbert transform

這個演算法，是利用Empirical Mode Decomposition(EMD)將原訊號拆解成數個Intrinsic Mode Functions (IMF)。今天我整理一下以音高為D4的小提琴為輸入所做的實驗結果。

整個 Hilbert Analysis流程如下圖所示(謝志敏, 2007)。

一開始先做 EMD，先找出整段訊號的 local maxima & minima，然後用 cubic spline line分別造出envolope，最後再將這兩個envelope取平均，即為第一個分量；依此類推，直到這個平均後的值趨近於水平線時，該訊號即為第一個 IMF。收斂條件依定義為一名為 SD 的式子，不過實驗的程式是執行 10 次 iterations。

小提琴做完的結果如下圖所示。由上至下依次為原音(當作是IMF 1)、IMF 2, 3, 4, 5, 6。音檔在這裡，可直接下載。

聽過音檔後，大家應該不難發現，IMF 2 的頻率較高，IMF 5 聽起來像是心跳聲，噗通一下就沒了。其實依傳統EMD作法，解出來的 IMF 順序，其瞬時頻率是由高往低的，有點類似像 band pass filter。由圖可知，IMF 4的頻率是最接近原音音高的地方，所以能量最大，而 IMF 5只剩起頭音的部份有聲音。

小結：

IMF 5 只有起頭音跟後面一小段(?)有訊號，可能會是我要做 noise modeling 時所需要的元素。而年前老師要我改變 maxima & minima envelope的擷取方式，希望能先抓出較完整的 sine wave，目前做出來效果並不理想，一來是envelope要抓得很完美不好做，二來是 IMF 依舊有從高頻先被取出來的特性。

投影片：下載。

2009/02/20 Progressive Report

目前的實驗是先將頻率考慮進去，求得週期後，先從任意為起點，往後的 1 週期內找 local maximum，此點即為 peak value。下個起點，則由目前的 peak value 位置往後移動 2/3 週期，不直接移動一整個週期是怕有誤差，一直重複上列動作就可以找出所有 peak value；同理，也可以找出所有 valley value，最後結果如下。

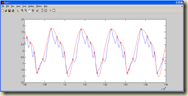
上圖的藍色 envelope 是原訊號，紅色 envelope 則是有 peak & valley 為點作 spline function 而成的結果。將藍色減掉紅色，就是下圖的藍色。

從上圖來看，紅色 envelope 還滿貼近原訊號的，本以為扣掉後剩下的訊號會變很少，但事與願違。原因是出在 spline function 造出來後雖然很貼近，但仍有些區域是差得較遠的，紅直線跟青直線分別是原本的 peak & valley 所對照下來的位置，這兩個位置扣掉後都是 0 ，但其他位置卻有相差到 +1 / –1 的大小。

接下來，我將試著將半週期內所有的 peak & valley，套用 monotonic increasing/decreasing 的條件後再看看結果。

0225-Memo:

• 觀察這個失敗的實驗，看看是否做無限迴圈後能擷取出f0。
• 找論文看有沒有人用HHT做修改來分析聲音。

2009/03/03 Progressive Report

我先給大家看一下上次提到的「半週期內所有的 peak & valley，套用 monotonic increasing/decreasing 的條件」的結果。

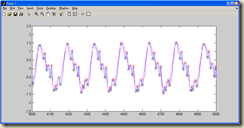
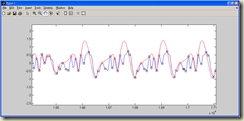
這個訊號的週期約在148-150個sample左右，f0差不多在297-300。大家可觀察到無論是紅點(peak)還是黑點(valley)，從最大值開始算半個週期內皆呈現 monotonic decreasing，下個半週期則呈現 monotonic increasing。粉紅色線為紅點及黑點所建連線的平均線。

不過，藍線減掉紅線的結果如下圖。

很明顯的，300hz 的波形還是有留一些能量，原因是因為粉紅色線的極值沒有緊緊貼在原訊號的極值上，導致減掉後仍留有能量，相較於其他波形的能量甚至還滿大的。

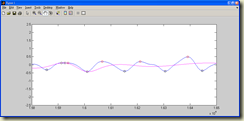
隔天，我試著將原訊號的極值同時加到peak/valley兩邊的陣列資料中，這樣照 spline function 時至少在極值的地方會重疊。結果如下圖。

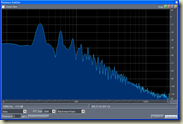
原訊號的頻譜:                             平均線的頻譜:

 

原訊號 - 平均線

已知問題及解法:

做完第一次後，剩下的訊號其300Hz, 600Hz, 900Hz 的能量明顯掉了許多，因此第二次再做時，不能再以原本的週期來作為 monotonic inc/dec 的判斷，否則造出來的spline function會有爆走問題，如下圖。解法: 先用簡單的pitch detection算出目前能量較大的週期後再做第二次實驗。

第二次                                       第三次

Bug: 找出在做第一次時16000-21000, 25000-33000 區域的振幅大小有一點小爆走的原因。(而且還只有下方有爆走)

2009/03/06

上面的Bug 解決了，原因出在有些區域的「最小極」沒有被列入spline function points，導致造出來的波形在某些情況下會有點誤差。

雖然問題解了，可是出來的結果還是跟上圖差不多，為了方便解釋一下原因請看下圖。

圖中有兩個紅圈圈，紅點跟黑點有全部找到，可是左紅圈內的結果卻比右紅圈內的結果較好，why? 其實這就是訊號的特性，左紅圈內的黑點較集中，所以 spline function 造出來的envelope較貼近原訊號，但右紅圈內的黑點較分散，所以會有波形振幅不一的情況。

這個「現象」目前我不將它當成「問題」，之前之所以成為「問題」的原因是在16000-18000這段的頻譜，在經過三、四次loop後高頻的能量不減反增，但現今已經沒這問題。這裡補一下圖：

0303版，第四個loop後剩下的波形，及27825點該frame的頻譜:

0306版的:

我將繼續往下做，讓週期是 adaptive 的，再看看結果如何。

2009/03/10

老師在3/7的留言中提出一個疑問: 「經過第一次decomposition後, peaks降低了, 可是noise floor也變大了. 這是甚麼原因呢?」

我紀錄一下大家的看法。

老師:

Spline function 是採用 non-uniform sampling 的作法，跟 Fourier Transform 觀念背道而馳，因而可能造成這種現象。(ps. 這邊不太懂 non-uniform sampling 可能造成哪些結果)

Spline function本身main lobe不夠尖，side lobe也不夠小，換成 sinc function 可能會比較好。

DNA:

有時候別太相信 Cooledit …，它的db scale不知道到底對象是誰。

Showmin:

我翻了下課本，發現兩個訊號點對點相加時，能量本來就有可能會大於在頻率上的點對點相加，只要兩者 FFT 出來的實部係數or虛部係數異號。

|x1| + |x2| >= |x1+x2|

小結: 這種現象會不會影響結果還不知道，先紀錄一下。

最後貼一張圖，我在範圍介於 +-10 之間造一個 sinc(x)，而且只取15點。然後，用這15點座標來分別造出新的 sinc 跟 spline，出來的結果如上圖，spline function較平緩。下圖則是上圖做 abs(fft(x)) 的結果。

2009/03/17

1. ACF用來判斷pitch period不適用於我們的實驗，因為我們無法將某一pitch的能量完全扣除乾淨。

2. 接著我讓pitch period隨著loop數減少，前兩圈的結果如下。

 

即使我將起始點位移的距離改小，還是有一些點沒有找到。

是的，這是bug，解決方法很簡單：在找一個週期內的極值時，順手將這個值加到 set 中。之前是只有在判斷 monotonic increasing/decreasing 時才會加進去。當然，在這種情況下極值可能會被加到不只一次，但不影響程式執行的。最新結果如下：

3. spline function effect

這個問題前面就有提過，就是兩個點距離如果有點遠，但值卻差不多大，則spline function會凸出來。上面的結果雖是正常，但只要換到其他時間點來觀察，依然有問題。

這個圖的點其實都有找對了，但卻因 spline function 的特性造成有凸出來的 effect。

 

 

投影片下載：這裡

DNA:

何不試著在原訊號後面較穩定的地方找一段完整週期訊號，以此為 template，然後將原訊號拿來減掉這個template，template的能量可隨著該frame而調整。

2009/03/18

由上面第3點的結果我們可以發現，在訊號的能量都差不多時(noise-like)，用新方法是滿容易因spline function爆走的，所以老師提供一個實驗方式，要我第一圈先用新方法，第二圈用EMD，看看做完EMD後能否再讓訊號「有起伏」。這個答案是肯定的，請看圖。

第1圈用新方法求得的平均線。

第二圈改用EMD，下圖為EMD做10次後的結果。

做完EMD後，用原訊號扣除上圖即為下圖。很明顯下圖的波形「有起伏」，那理論上再回頭用新方法來找應該很棒，可是為何平均線會找得沒有第一次好呢？這是因為第三圈的週期只剩 150/3 = 50，點的距離較寬而無法將最大值納入 min set，反之亦然，也無法將最小值納入 min set，所以平均線雖然沒有爆走，但卻沒那麼貼。

如果週期維持在150的話就會好多了，當然一樣會有spline function effect，而且點距離越寬越明顯。

第四圈，再做 EMD。

第五圈，再回頭用新方法。此時可以發現用新方法或用 EMD 效果都差不多了。

目前有些疑問，再找時間跟老師討論。